Unlock The Super Power of Polynomial Regression in Machine Learning

Polynomial regression is a supervised machine learning algorithm used on non-linear data with no linear correlation between variables. 

It is one of the most widely used machine learning algorithms on nonlinear data as it can solve the non-linear relationship between independent and dependent data and returns accurate results.

In this article, we will discuss polynomial regression, its core intuition, working mechanisms, code examples.

This will help one to understand the algorithm better and will help answer interview questions related to it very efficiently.

What is Polynomial Regression?

Polynomial regression is a type of regression analysis in which the relationship between the independent variable (usually denoted as "x") and the dependent variable (usually denoted as "y") is modelled as an nth degree polynomial. 

In other words, instead of fitting a linear function (y = mx + b) to the data points, a polynomial function (y = a + bx + cx^2 + ... + zx^n) is fitted to the data points.

Polynomial regression can be useful in cases where the relationship between the independent and dependent variables is nonlinear. 

For example, you have data on the price of a home and the square footage of the home. In that case, a linear regression model may not capture the true relationship between the two variables, as the relationship is likely to be curved rather than straight.

By using a polynomial regression model, we can better capture the curvature in the relationship between the two variables.

However, it's important to note that as the degree of the polynomial increases, the model becomes more complex and may overfit the data, leading to poor generalization performance on new, unseen data.

Polynomial regression can be implemented using various regression algorithms such as linear, ridge regression, and lasso regression. The choice of algorithm depends on the specific problem and the complexity of the polynomial model being fitted.

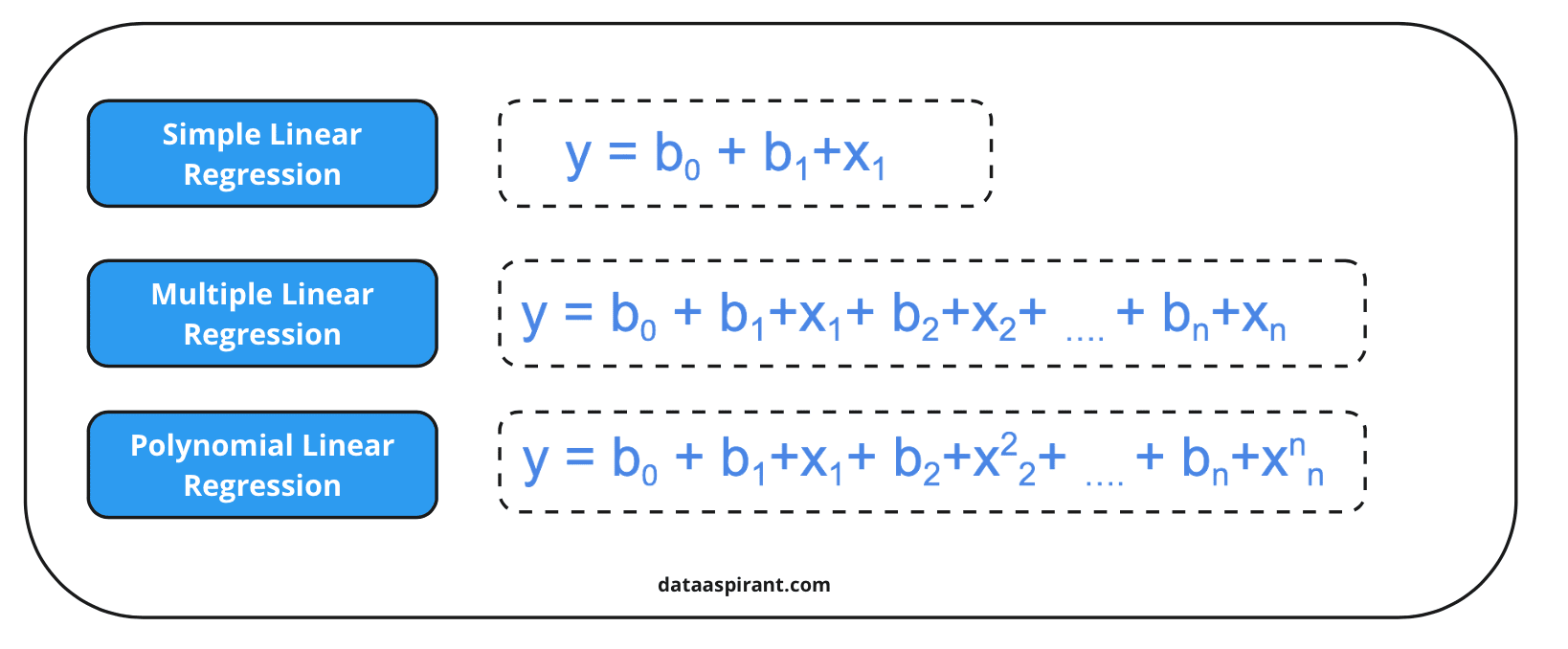
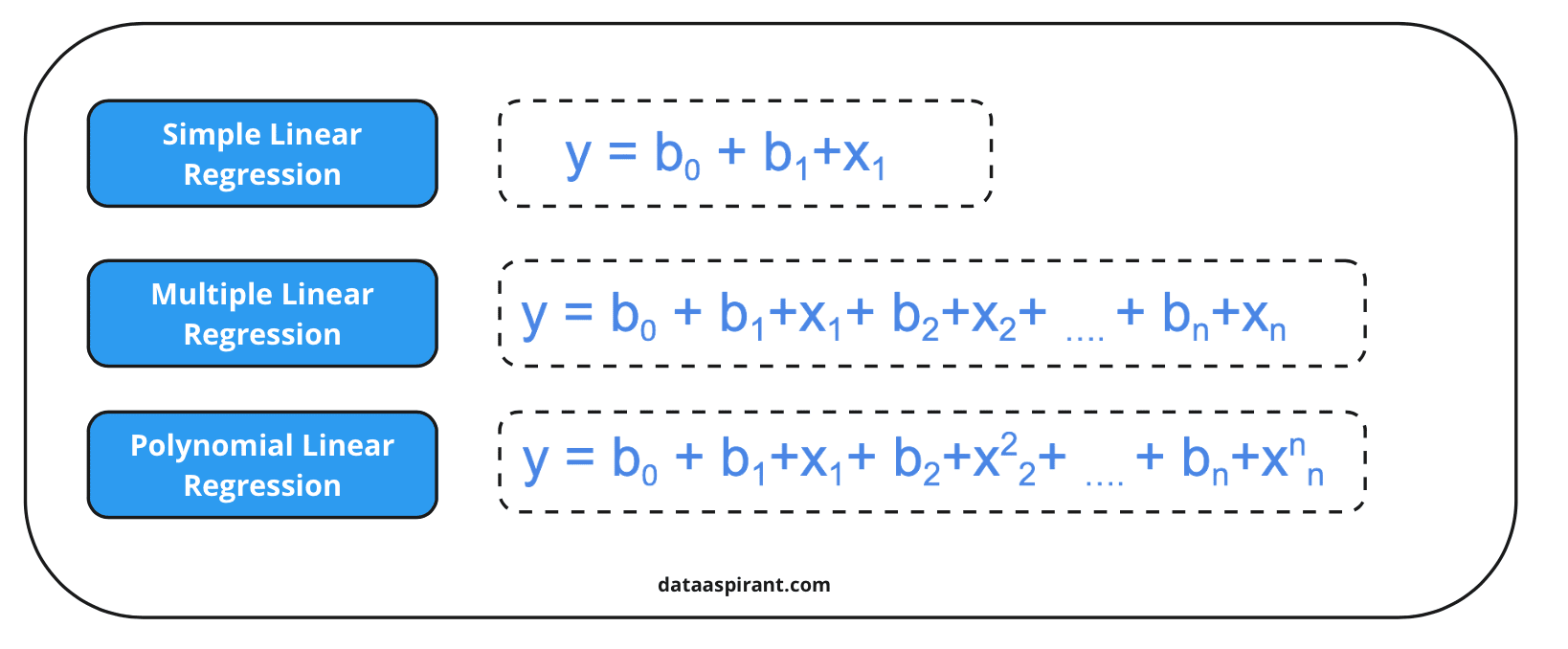
As we can see in the above image, the formula for polynomial regression is also the same as the simple linear regression and multiple regression; just one small difference is that polynomial regression will have a degree or polynomial function that will be applied to the features X1, X2, X3, etc. 

This degree of the polynomial will make the regression able to solve nonlinear relationships between data.

One core assumption of polynomial regression is that there should not be multicollinearity present here, which means there should not be a correlation between independent features. 

They all should be dependent and not correlated. Also, having a normal distribution in the dataset is better for better results.

Types of Polynomial Regression

We can classify the polynomial regression on the basis of its degree. The polynomial equation can have any degree starting from 1 to n.

1. Linear: A polynomial regression having degree one is known as linear polynomial regression.
2. Quadratic: A polynomial regression with polynomial degree two is known as quadratic polynomial regression.
3. Cubic: A polynomial regression with three is known as cubic polynomial regression.

Linear Regression Vs Polynomial Regression

Let us understand the difference between linear and polynomial regression.

Let’s suppose you have a dataset that is a kind of nonlinear dataset and does not have a linear relationship between independent and dependent variables. 

Now here, you applied linear regression, found the best-fit line, and calculated the error for the algorithm. 

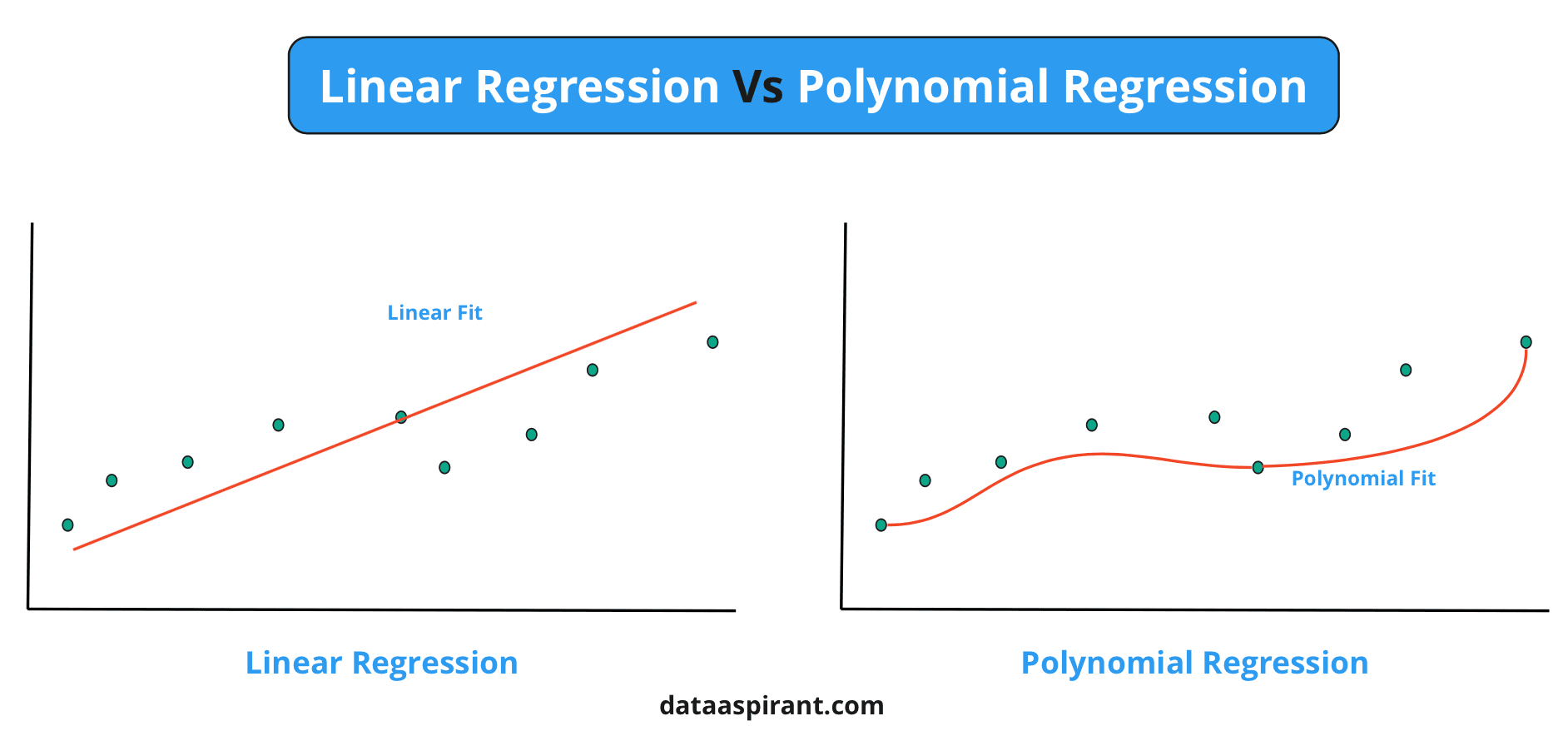
Here you will find that the algorithm will not play well, and there will be lots of errors in the best-fit line as the line would not be a better predictive line for a nonlinear dataset the data is nonlinear and the line would be linear.

Now you applied the polynomial regression and again calculated the errors and best-fit line; as the polynomial regression can be applied to non-linear data, the algorithm will study the data and generate the best-fit line, which will be non-linear and best fitting to data for prediction.

As we can see in both cases, both cases or algorithms work better if the situations or the type of the data is according to their assumptions and working mechanisms. 

Here, the linear regression would have been performing better if the data had been linear. At the same time, the polynomial regression performs better on nonlinear data.

Building Polynomial Regression Model

Now that we have an idea about polynomial regression, let us try to understand the code of the same.

The polynomial regression can be easily applied to any dataset using the Sci-kit Learn library. You can directly import and use the polynomial regression from sklearn.preprocessing class.

Step 1: Import Required Libraries

In order to apply and implement polynomial regression, we need first to import some of the required libraries to make the process easier and more efficient.

Step2: Defining the Data

Now let us take a popular tips dataset with polynomial features. We will have an independent and dependent feature here: X and Y.

Step 3: Polynomial regression

Let us split the data into train and test datasets and apply polynomial of degree two.

Step 4: Applying Linear Regression

Let us apply the linear regression now to the transformed dataset.

Step 5: Mean Squared Error

Let us print the Mean Squared Error of the model.

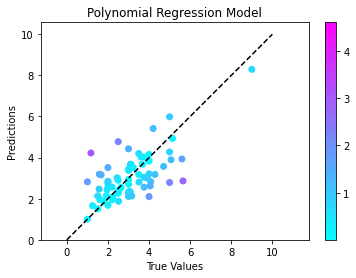
Step 6: Visualization Results

Let us visualize the results we obtained from the model, in order to get an idea about the performance of the model. 

As we can see in the above code, we have imported the Polynomial features class from SKLearn, which will transform the data features into polynomial features.

Then simple linear regression is used to get the best-fit line for the prediction purpose. 

Note that here the degree of polynomial should be the optimal value according to the type of data, and the polynomial features should be passed to linear regression to get better results.

How to Select the Best Degree for Polynomial?

As the polynomial regression can be applied to the nonlinear data, if the degree of polynomial plays a major role in the final results.

As the degree of the polynomial changes, then the performance will also change.

Experiment with the degree of the polynomial. You will get to know that with a very high value of the degree of the polynomial, the overfitting case is happening where the model is performing accurately and giving 100% accuracy on training data and performs poorly on testing data.

Also, if you select the very low value of the degree of the polynomial, you will notice the underfitting case where the model will not perform better either on training or testing data.

In such cases, we should try from one particular small value of degree or polynomial and then observe the performance of the algorithm.

If it performs poorly, then it increases the value of a degree. The same thing can be done in a loop to get the optimal value of the degree.

Key Points to Remember 

• Polynomial regression is a type of regression that can be applied to nonlinear data.
• It is not necessary that polynomial regression will always perform better than linear regression, but in the case of nonlinear datasets, the algorithm surely performs better.
• The polynomial regression can be classified into various classes based on the degree of the polynomial.
• The degree of a polynomial can be selected by experimenting with the algorithm's performance with carefully increasing or decreasing the degree's value.

Conclusion

In this article, we discussed polynomial regression, its core intuitions, mathematical formulations, the difference between linear and polynomial regression.

We also build polynomial regression with python code, and disucssed the proper method for selecting the degree of the polynomial for avoiding overfitting and underfitting.

This will help one to understand the polynomial regression very clearly and will also help to apply the algorithm to nonlinear data.

Recommended Courses