If maths is the magician, then the central limit theorem is like a magic trick that happens when you add up lots of little things!

Didn’t understand? Well, let’s dive deep into this 😉

Anyone studying statistics eventually comes across the concept of the Central Limit Theorem. While some find it difficult to understand, it is a fundamental statistical concept that can be broken down into simpler terms. 

This guide will explain the Central Limit Theorem and how it works, making it perfect for beginners who may be struggling with the concept.

Before we go further, Let’s see the table of contents for this article.

What is Central Limit Theorem?

Let's say you have a bunch of friends, and you want to see how tall they are. You could measure each friend's height, and then find the average height of all your friends.

But what if you don't have time to measure every single friend?

Here's where the central limit theorem comes in. It says that if you add up a bunch of random things, like the heights of your friends, the total will look like a bell-shaped curve. This curve is called a normal distribution.

So, let's say you only measure the height of a few of your friends, maybe 5 or 10 of them. Even though you haven't measured all of your friends, if you add up all their heights and plot them on a graph, you'll see that the curve looks like a bell shape.

The cool thing is that the central limit theorem works for many things, not just height. It works for things like test scores, the number of people who visit a website, or the weight of apples in a basket.

So, to sum it up, the central limit theorem is a magic trick that says if you add up lots of little things, like the heights of your friends, the total will look like a bell-shaped curve.

Using Central Limit Theorem in Statistics and Data Science

The central limit theorem (CLT) is a fundamental concept in statistics and data science that helps solve various problems. Some of the key problems that the CLT solves are:

1. Estimating Population Parameters: The CLT helps us estimate population parameters, like the mean and standard deviation, by using a sample of the data. This is important because it allows us to make inferences about the entire population based on a smaller sample.
2. Hypothesis Testing: The CLT is used to test hypotheses about population parameters, such as whether two means are statistically different or not.
3. Confidence Intervals: The CLT helps us create confidence intervals, which are ranges of values that we are confident contain the true population parameter.
4. Model Fitting: The CLT is also used in model fitting, where it helps us estimate the parameters of a statistical model by using data.

Limitations of the Central Limit Theorem

The CLT has some limitations. These include

1. Sample Size: The CLT assumes that the sample size is large enough for the normal distribution to emerging. The CLT may not be applicable if the sample size is too small.
2. Independence: The CLT assumes that the samples are independent of each other. If the samples are not independent, the CLT may not be applicable.
3. Outliers: The CLT is sensitive to outliers, which can skew the distribution and affect the accuracy of the results.
4. Non-Normal Distributions: The CLT only applies to populations with a normal distribution. The CLT may not be applicable if the population is not normally distributed.

Central Limit Theorem Assumptions

The central limit theorem has below four key assumptions. These assumptions are largely talk about samples, sample sizes, and the population of data.

1. Sampling is successive: Some sample units are common with sample units selected on previous occasions.
2. Sampling is random: The sample selection must be random so that they have the same statistical possibility of being selected.
3. Independent Samples: The selections or results from one sample should not affect future samples or other sample results.
4. Samples should be limited: If sampling is done without replacement, the sample should be no more than 10% of the population. In general, larger population sizes warrant the use of larger sample sizes.

What are the 3 main rules of Central Limit Theorem

The 3 main rules of central limt theorem are Independence, Sample Size, Population distribution.  Let's understand these in detail. 

Independence

The observations in the sample should be independent of each other. Independence ensures that the sample is representative of the population and that the observations in the sample are not affected by each other.

For example, if we are sampling the heights of students in a classroom, we would want to ensure that each student's height is independent of the height of other students.

If two students are related, their heights may be correlated, and the sample may not represent the population.

Sample Size

The sample size should be sufficiently large. This ensures that the sample mean is a good estimate of the population's mean. If the sample size is too small, the sample mean may not be representative of the population mean.

The exact sample size required depends on the underlying distribution of the population. If the population distribution is normal, a sample size of at least 30 is generally sufficient.

However, if the population distribution is highly skewed or has heavy tails, a larger sample size may be required to ensure that the CLT applies.

Population Distribution

 The population distribution should be finite or well-defined. This means that the population should have a mean and a finite variance. If the population distribution is undefined or infinite, the CLT may not apply.

For example, if we are sampling the number of cars passing through a toll booth daily, we would assume that the population has a finite mean and a finite variance.

If we are sampling the number of bacteria in a petri dish, we would assume that the population has a finite mean and a finite variance.

Why n ≥ 30 Samples In CLT

A sample size of 30 is often used as a rule of thumb in statistical practice for applying the Central Limit Theorem (CLT). However, it's important to note that the actual required sample size can vary based on the population distribution and the desired level of precision.

In general, a larger sample size will provide a more accurate estimate of the population mean. Still, there are several reasons why a sample size of at least 30 is often considered a good starting point

Normality Assumption

One reason for the sample size of 30 or more is that it helps to fulfill the normality assumption, which is one of the requirements for the CLT to apply.

When the sample size is less than 30, the distribution of the sample mean may not be normal, and therefore the CLT may not hold.

However, when the sample size is greater than or equal to 30, the distribution of the sample mean tends to be approximately normal, regardless of the shape of the population distribution.

Large Enough to Capture Variation

Another reason for a sample size of at least 30 is that it is generally large enough to capture the variation in the population.

A sample size of less than 30 may not provide enough information about the population, and the estimate of the population mean may be too variable to be useful.

A larger sample size can help to reduce this variability and provide a more accurate estimate of the population mean.

Sufficient Precision

A sample size of 30 or more can also provide sufficient precision in estimating the population mean.

With a larger sample size, the standard error of the sample means decreases, which means that the sample mean is more likely to be close to the population mean.

This increased precision can be useful in making more accurate inferences about the population.

Understanding the Maths behind Central Limit Theorem

The CLT theorem tells us that when we take a large enough sample size (n) from any population, the sample means will approximate a normal distribution, regardless of the distribution of the population. 

This is true as long as the sample is random, independent, and identically distributed (iid).

The CLT can be expressed mathematically as follows:

Let X1, X2, ..., Xn be a random sample of size n from any population with mean μ and standard deviation σ.

Then, as n approaches infinity, the sampling distribution of the sample mean X̄ approaches a normal distribution with mean μ and standard deviation σ/√n.

In other words, the mean of the sampling distribution of the sample mean is equal to the population mean, and the standard deviation of the sampling distribution of the sample mean is equal to the population standard deviation divided by the square root of the sample size.

For example, let's say we want to estimate the average height of all students in a school. We take a random sample of 100 students and measure their heights. The mean height of our sample is 5 feet 8 inches, with a standard deviation of 3 inches.

According to the CLT, as we increase the sample size, the distribution of the sample means will approach a normal distribution. 

Let's take another random sample of 1,000 students and measure their heights.

The mean height of this new sample will be normally distributed with a mean equal to the population mean (the true average height of all students in the school) and a standard deviation equal to the population standard deviation divided by the square root of the sample size (in this case, 3 inches/√1000 ≈ 0.09 inches).

The CLT is a powerful mathematical concept that is used in many areas of statistics and data science to make inferences about populations based on sample data.

Remembering the CLT's assumptions and limitations to ensure accurate and reliable results is important.

Real-world applications

The Central Limit Theorem has many real-world applications, particularly in the field of statistical analysis.

For example, it can be used to conclude a population by making inferences from a sample group. 

This is important for drawing accurate conclusions about public opinion or customer preference based on survey data.

In addition, CLT is also used in quality control to make decisions about whether or not to accept batches of manufactured products by analyzing samples taken from the batch. 

Therefore, understanding the Central Limit Theorem can be invaluable in many different industries and fields where statistical analysis is used.

Limitations and Alternatives to the Central Limit Theorem (CLT)

While the Central Limit Theorem is a powerful tool for statistical analysis, its application has certain limitations.

 For example, it assumes that the sample size is large enough and that the observations in the sample are independent of each other. 

In addition, there may be situations where the population being studied does not follow a normal distribution or has extreme outliers, which could impact the validity of using CLT.

Alternatives to CLT include bootstrapping and permutation tests, which can also provide accurate results when studying a population.

It’s important to understand the limitations and alternatives to CLT when conducting statistical analysis to ensure accurate conclusions are drawn from data.

CLT Python Implementation

Let's say we have a population of numbers with a uniform distribution between 0 and 1, and we want to see how the sample mean changes as we increase the sample size. 

We can use the CLT to predict that the sample mean will approach a normal distribution as the sample size increases.

Not let's write script to create the graphs.

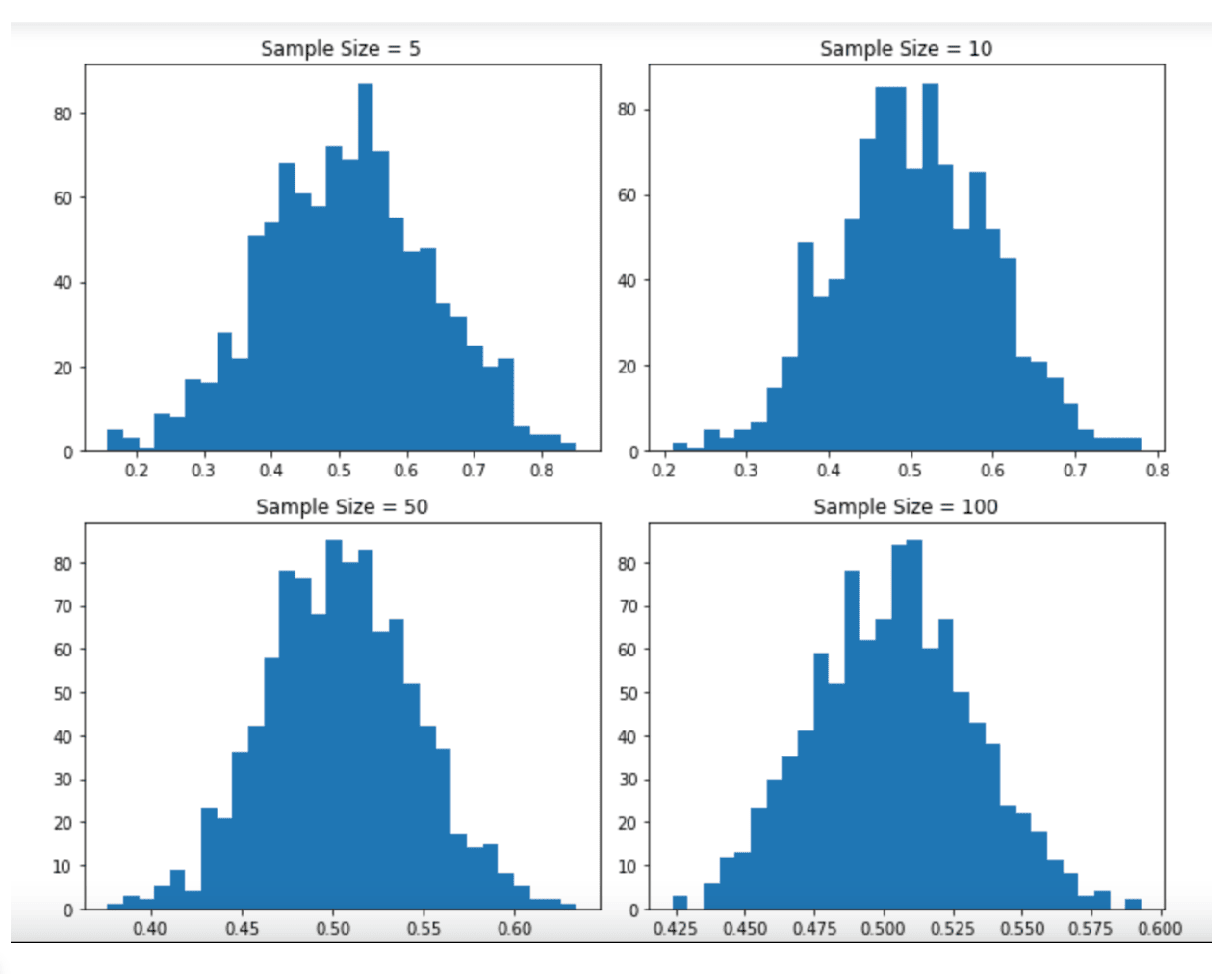
In this code, we first generate a population of 10,000 numbers with a uniform distribution between 0 and 1 using the NumPy random. uniform function.

We then define a function called calculate_sample_means that takes a sample size and the number of samples to draw and returns a list of sample means.

This function randomly selects a sample of the specified size from the population without replacement using the NumPy random. choice function calculates the mean of the sample using the NumPy mean function and appends the sample mean to a list.

We then loop over different sample sizes (5, 10, 50, and 100) and calculate the sample means for each sample size using the calculate_sample_means function. We store the sample means in a dictionary called sample_means.

Finally, we plot histograms of the sample means for each sample size using the Matplotlib hist function. We use the tight_layout function to adjust the spacing between the subplots and the show function to display the plot.

When we run this code, we should see a plot with four subplots, each showing the histogram of the sample means for a different sample size.

We should see that as the sample size increases, the distribution of the sample means becomes more normal, which confirms the prediction of the CLT.

Conclusion

In conclusion, the Central Limit Theorem is a fundamental concept in statistics and data science that helps solve a variety of problems such as estimating population parameters, hypothesis testing, confidence intervals, and model fitting.

However, the CLT has some limitations, including sample size, independence, outliers, and non-normal distributions. The CLT assumptions include sampling, random selection, independent samples, and limited samples.

The three main rules of the CLT are independence, sample size, and population distribution, and a sample size of 30 is often used as a rule of thumb.

Despite its limitations, the CLT is a powerful tool in statistical analysis that allows us to make inferences about populations based on smaller sample sizes.

Frequently Asked Questions (FAQs) On Central Limit Theorem

1. What is the Central Limit Theorem (CLT) in Statistics?

The Central Limit Theorem is a fundamental statistical concept that states that the distribution of sample means approximates a normal distribution (bell-shaped curve), regardless of the shape of the population distribution, as the sample size becomes large.

2. Why is the Central Limit Theorem Important?

The CLT is important because it allows for making inferences about population parameters using sample statistics. It is the foundation for many statistical procedures and hypothesis tests.

3. Does the CLT Apply Only to Normal Distributions?

No, one of the key points of the CLT is that it applies regardless of the population’s distribution shape. Whether the population distribution is normal, skewed, or has any other form, the sampling distribution of the mean will tend to be normal with a sufficiently large sample size.

4. What is Considered a 'Large' Sample Size in CLT?

While there's no fixed number, a sample size of 30 or more is often considered sufficient for the CLT to hold, but this can vary depending on the actual distribution of the data.

5. How Does Sample Size Affect the Central Limit Theorem?

The larger the sample size, the closer the sample means will be to a normal distribution. With smaller sample sizes, the approximation to normality might not be accurate, especially if the population distribution is highly skewed.

6. Can the CLT be Applied to Any Type of Data?

The CLT is generally applied to quantitative data. It is important for the data to be independent and identically distributed.

7. What is the Role of the CLT in Confidence Interval Construction?

The CLT allows us to use the normal distribution to construct confidence intervals for population means, even when the population distribution is not normal.

8. Does the Central Limit Theorem Apply to Proportions and Variances?

Yes, the CLT applies to sample proportions and variances as well. The distribution of sample proportions and sample variances will approximate a normal distribution as the sample size increases.

9. How is the CLT Used in Hypothesis Testing?

In hypothesis testing, the CLT allows us to use the normal or t-distribution to test hypotheses about population means, even when the population is not normally distributed.

10. Are There Limitations to the Central Limit Theorem?

 The main limitation is the requirement of a sufficiently large sample size. Additionally, the CLT does not apply to certain statistics, like the median, which do not necessarily converge to a normal distribution.

11. How Does the CLT Relate to the Law of Large Numbers?

 While the Law of Large Numbers tells us that the sample mean converges to the population mean as the sample size increases, the CLT tells us about the shape of the distribution of the sample mean.

12. Is the Central Limit Theorem Relevant in Real-World Applications?

 Absolutely. The CLT is used in various real-world applications, including quality control, election polling, financial market analysis, and many areas of scientific research.

Recommended Courses